پایداری نوسان و مقاومت منفی

پایداری نوسان و مقاومت منفی

پایداری

معادله مشخصه معادله دیفرانسیل حاکم بر یک مدار مرتبه دوم دارای دو ریشه است. اگر این دو ریشه در سمت چپ صفحه مختلط قرار داشته باشند پاسخ مدار پایدار است (پایداری). یعنی در حالت ورودی صفر پاسخ مدار در زمان بی نهایت به سمت صفر میل خواهد کرد. در حالت پایداری ثابت میرایی بزرکتر از صفر است و بر مبنای دو پارامتر ثابت میرایی و فرکانس تشدید سه وضعیت مختلف خواهد داشت:

۱- میرایی شدید: در این حالت ثابت میرایی از فرکانس تشدید بزرگتر است در نتیجه معادله مشخصه دو ریشه حقیقی و منفی دارد. در چنین شرایطی پاسخ مدار به سرعت میرا می شود.

۲- میرایی بحرانی: در این حالت ثابت میرایی برابر فرکانس تشدید است در نتیجه معادله مشخصه دو ریشه حقیقی و منفی دارد که این دو ریشه مقداری برابر دارند.

۳- میرایی ضعیف: در این حالت ثابت میرایی از فرکانس تشدید کوچکتر است در نتیجه معادله مشخصه دو ریشه مختلط با مقدار حقیقی منفی دارد. در چنین شرایطی پاسخ مدار RLC به صورت نوسانی میراشونده است.

نوسان

اگر ثابت میرایی برابر صفر باشد پاسخ ورودی صفر مدار نوسانی است و به این مدار، مدار تشدید میگویند. در این حالت ثابت میرایی برابر صفر است در نتیجه معادله مشخصه دو ریشه موهومی دارد که اندازه آنها برابر فرکانس تشدید است. در چنین شرایطی پاسخ مدار نوسانی است. این حالت را می توان حالت خاصی از میرایی ضعیف در نظر گرفت.

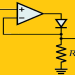
مقاومت منفی و نا پایداری

اگر مقدار مقاومت در مدار RLC منفی باشد مدار ناپایدار خواهد بود و در زمان بی نهایت پاسخ ورودی صفر آن به بی نهایت میل خواهد کرد. در چنین مداری ثابت میرایی کوچکتر از صفر است و بنابراین ریشه های معادله مشخصه در سمت راست صفحه مختلط قرار دارند.

[۱] Hayt, William, Jack Kemmerly, and Steven Durbin. Engineering ciRLuit analysis

دانلود جزوه

دانلود ویدئو

(۲۲۶۷)